Why Quick Sort Is Faster than Heap Sort?

Wed, Oct 2, 2019

Why Quick Sort?

I was reviewing sorting algorithm for my interview. The question just popped up in my mind when I was peeking the cheat sheet.

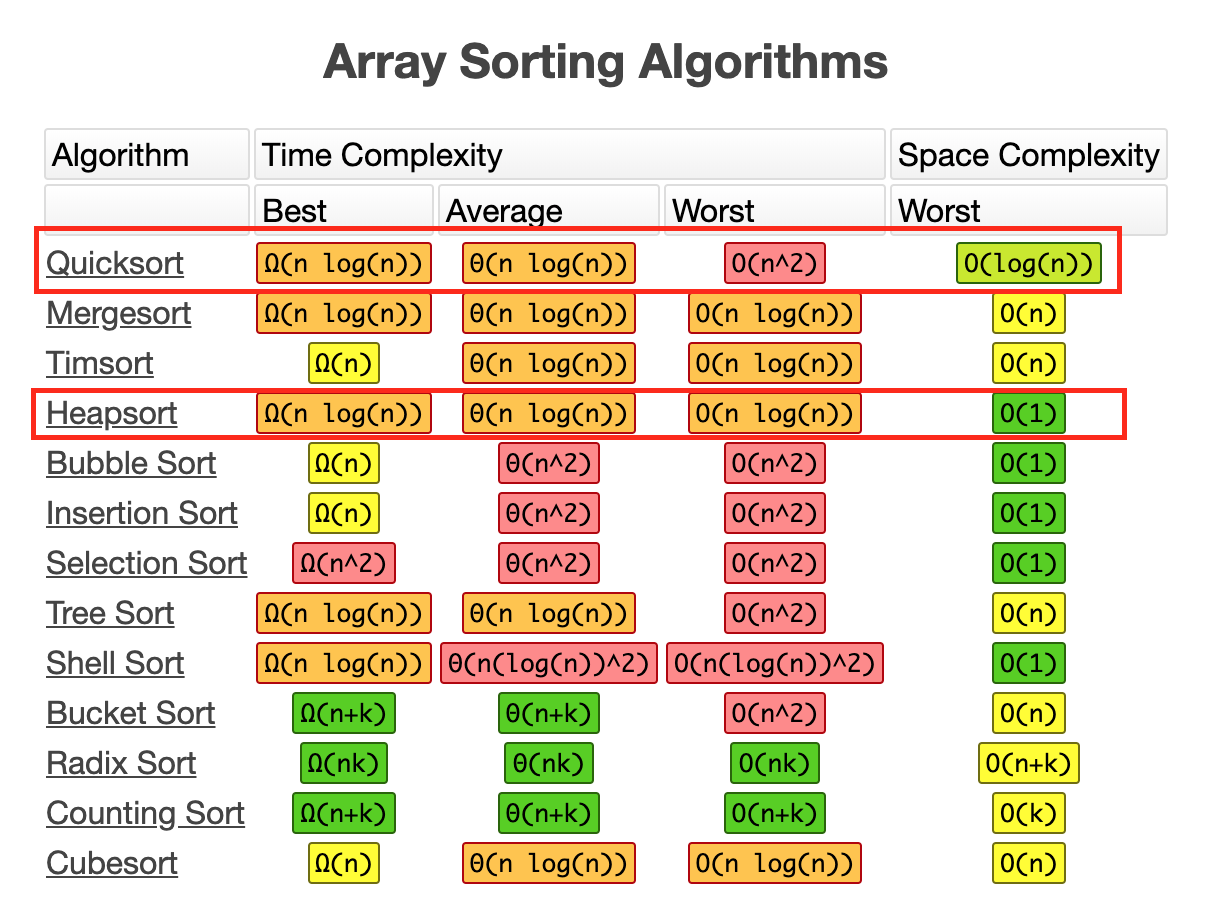[1]

You can see the best, average and worst time complexity of heap sort are all O(n logn) but it’s O(n^2) for worst of quick sort.
Then why do we always use quick sort? Since quick sort can’t beat heap sort in any cases, not even in space complexity.
I don’t see any advantages of choosing quick sort.

Time Complexity

Let’s review time complexity. Here is the definition from Wikipedia [2]:

In computer science, the time complexity is the computational complexity that describes the amount of time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to differ by at most a constant factor.

I’d like to focus on this sentence: supposing that each elementary operation takes a fixed amount of time to perform.
That means we do actually ignore the real world running time. It’s okay to do this since time complexity is used to describe the growth rate between an algorithm and it’s input size.

Let’s take a look at another thing: constant time [3]:

An algorithm is said to be constant time (also written as O(1) time) if the value of T(n) is bounded by a value that does not depend on the size of the input. Despite the name “constant time”, the running time does not have to be independent of the problem size, but an upper bound for the running time has to be bounded independently of the problem size. For example, the task “exchange the values of a and b if necessary so that a≤b” is called constant time even though the time may depend on whether or not it is already true that a ≤ b. However, there is some constant t such that the time required is always at most t.

Now, we should focos on this one: despite the name "constant time", the running time does not have to be independent of the problem size, but an upper bound for the running time has to be bounded independently of the problem size.
For example, take a look at the code below:

func sum(num []int) int {
    count := 0
    for _, v := range num {
        count += v
    }

    for i := 0; i < 1000; i++ {
        for j := 0; j < 1000; j++ {
            fmt.Println("constant operation here!")
        }
    }

    return count
}

What’s the time complexity you would say about this piece of code? O(n)? O(n^2)? (where n is the size of slice num)
We all know the time complexity is O(n) though there is a nested loop which runs a million times.
Why we can just drop the nested loop here? No matter how we change the size of input, the running time of the nested loop is all the same. That is, an upper bound for the running time has to be bounded independently.

Non-negligible Constant

I wrote quick sort and heap sort and here is the code:
Quick sort:

func quickSort(numbers []int, left, right int, c *Comparer) {
	if c.lessEqual(right, left) {
		return
	}

	pivot := numbers[left]
	i := left
	for j := left + 1; j <= right; j++ {
		if c.less(numbers[j], pivot) {
			i++
			c.swap(numbers, i, j)
		}
	}
	c.swap(numbers, i, left)

	quickSort(numbers, left, i-1, c)
	quickSort(numbers, i+1, right, c)
}

Heap sort:

func heapSort(heap []int, c *Comparer) {
	end := len(heap) - 1

	// build max heap
	for i := len(heap) / 2; i >= 0; i-- {
		heapify(heap, i, end, c)
	}

	// sort heap
	for i := end; i > 0; i-- {
		c.swap(heap, 0, i)
		heapify(heap, 0, i-1, c)
	}
}

func heapify(heap []int, i, end int, c *Comparer) {
	left := 2*i + 1
	if c.less(end, left) {
		return
	}

	target := left
	right := left + 1

	if c.lessEqual(right, end) && c.less(heap[left], heap[right]) {
		target = right
	}

	if c.less(heap[target], heap[i]) {
		return
	}

	c.swap(heap, i, target)
	heapify(heap, target, end, c)
}

Let’s run it and record the running time (I ran it 10 times for each size of input and average it).
Here is the result:

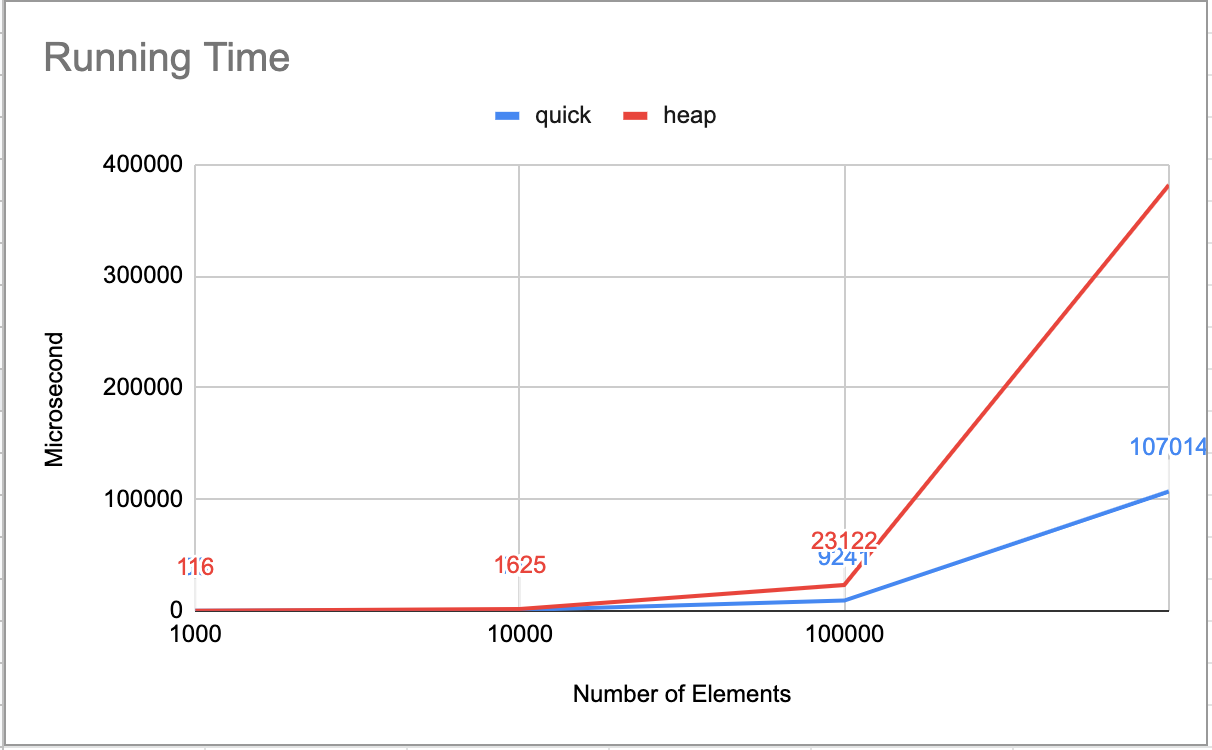
Actual number (first row represents the input size):

Running time (in microsecond)
#       1000    10000   100000  1000000
Quick   65      680     9178    104027
Heap    138     1652    21579   357418

You can see that quick sort is 2-3 times faster than heap sort.
Why this happens?
Sorting algorithm basically does two things: comparison and swapping. Let’s dig more from it.

You may have noticed there is a strange struct Comparer in the code above. I built this for counting the number of swapping and comparison.

func (c *Comparer) less(i, j int) bool {
	c.compareCount++

	if i < j {
		return true
	}

	return false
}

func (c *Comparer) lessEqual(i, j int) bool {
	c.compareCount++

	if i <= j {
		return true
	}

	return false
}

func (c *Comparer) swap(numbers []int, i, j int) {
	c.swapCount++

	numbers[i], numbers[j] = numbers[j], numbers[i]
}

Now let’s see the result:
Swapping:

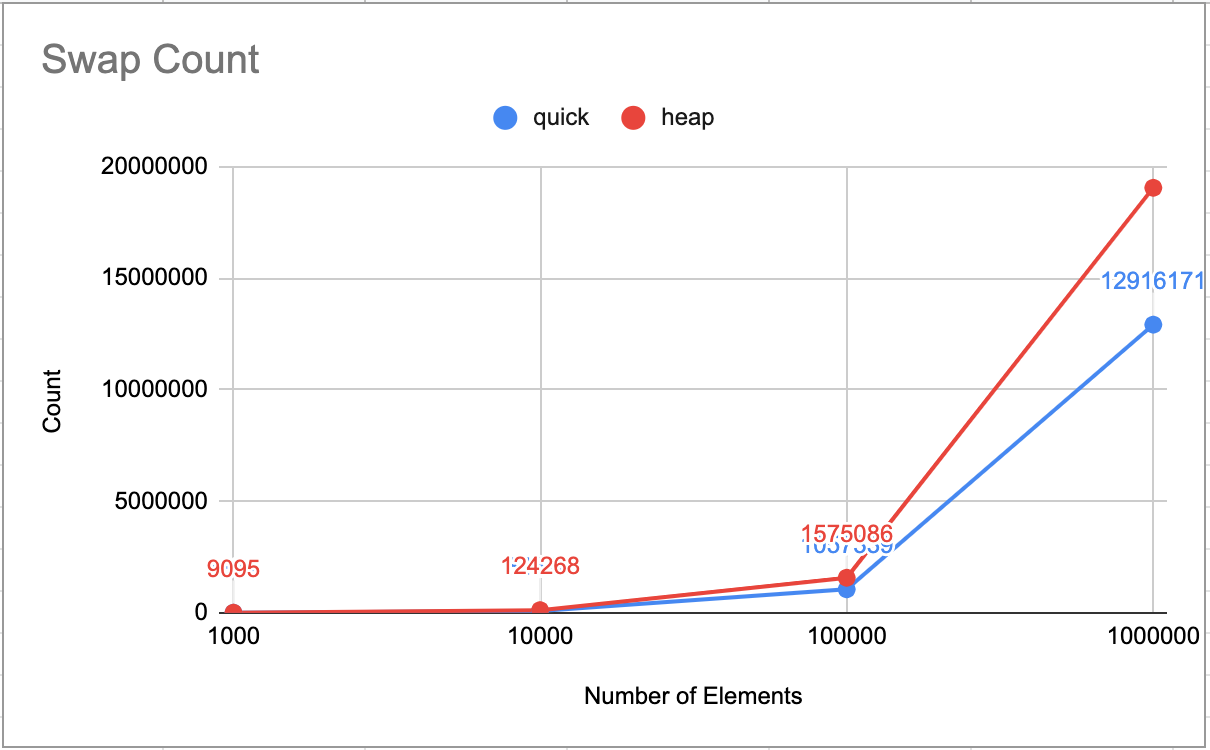
Acutal number:

Swap
#       1000    10000   100000  1000000
Quick   6121    84340   1059759 12768393
Heap    9081    124193  1574975 19047943

Comparison:

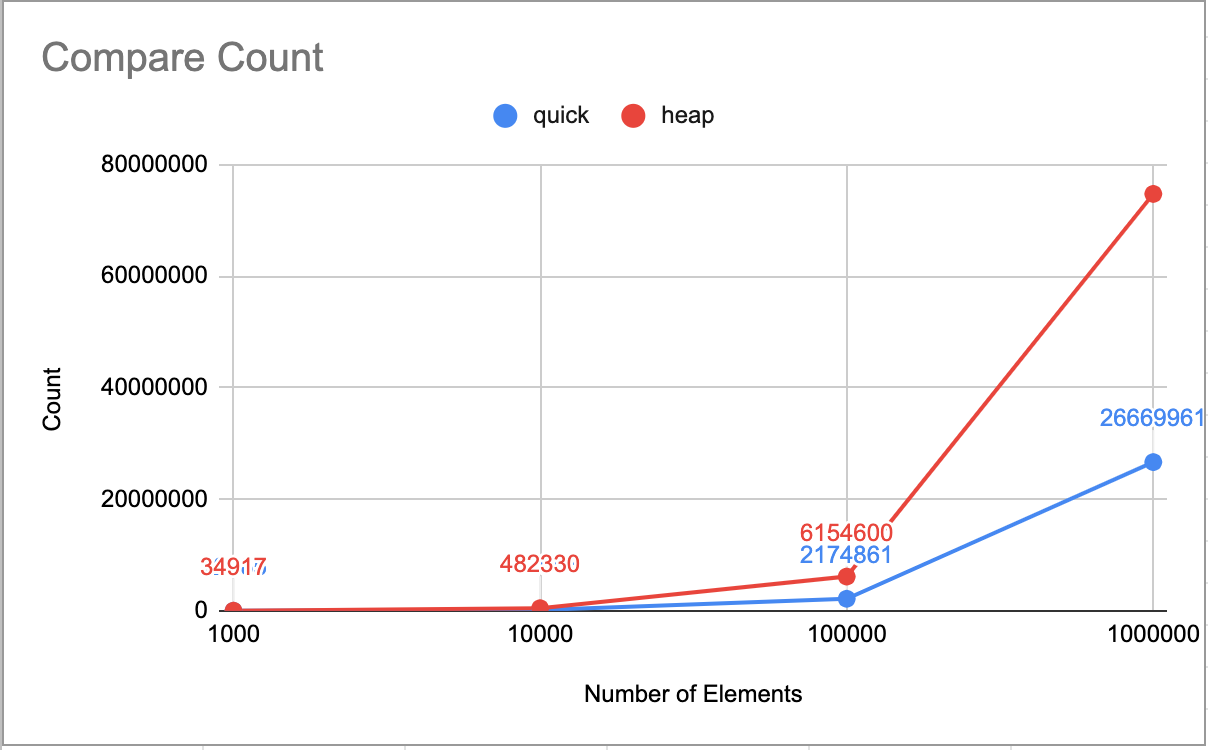
Actual number:

Comparison
#       1000    10000   100000  1000000
Quick   12054   171241  2171008 26372074
Heap    34868   482183  6154440 74738690

The numbers swapping and comparison of quick sort are far less than heap sort.
I think there are two reasons for this.
First, when we talk about time complexity, we actually talk about the input size and it’s running time. More precisely, the growth rate of running time and input size. We just drop all “fixed” operation.
Second, as I mention above, time complexity supposes every elementary operation takes a fixed amount of time and I reckon that swapping takes more time than comparison.
Besides these two reasons, we can even consider hardware level things such as memory locality or CPU cache line.
In other words, heap sort does too many useless swapping. Heap sort swaps elements for only maintaining “heap” structure. On the other hand, quick sort swaps elements for finding which one is greater or less than pivot and somehow this is really doing “sorting”.

Conclusion

Time complexity is a way to describe how running time of an algorithm grows. Though the input size is the dominant factor, we still have to keep an eye on those “non-negligible” constant.
This page[4] lists what sorting algorithm of a language uses. Most of them are hybrid algorithm for generality.

Reference

Appendix

package main

import (
	"fmt"
	"math/rand"
	"reflect"
	"time"
)

type Comparer struct {
	swapCount    int
	compareCount int
}

func (c *Comparer) less(i, j int) bool {
	c.compareCount++

	if i < j {
		return true
	}

	return false
}

func (c *Comparer) lessEqual(i, j int) bool {
	c.compareCount++

	if i <= j {
		return true
	}

	return false
}

func (c *Comparer) swap(numbers []int, i, j int) {
	c.swapCount++

	numbers[i], numbers[j] = numbers[j], numbers[i]
}

func getRandomSlice(n int) []int {
	source := rand.NewSource(time.Now().UnixNano())
	r := rand.New(source)
	s := make([]int, n)
	for i := range s {
		s[i] = r.Intn(n)
	}

	return s
}

func heapify(heap []int, i, end int, c *Comparer) {
	left := 2*i + 1
	if c.less(end, left) {
		return
	}

	target := left
	right := left + 1

	if c.lessEqual(right, end) && c.less(heap[left], heap[right]) {
		target = right
	}

	if c.less(heap[target], heap[i]) {
		return
	}

	c.swap(heap, i, target)
	heapify(heap, target, end, c)
}

func heapSort(heap []int, c *Comparer) {
	end := len(heap) - 1

	// build max heap
	for i := len(heap) / 2; i >= 0; i-- {
		heapify(heap, i, end, c)
	}

	// sort heap
	for i := end; i > 0; i-- {
		c.swap(heap, 0, i)
		heapify(heap, 0, i-1, c)
	}
}

func quickSort(numbers []int, left, right int, c *Comparer) {
	if c.lessEqual(right, left) {
		return
	}

	pivot := numbers[left]
	i := left
	for j := left + 1; j <= right; j++ {
		if c.less(numbers[j], pivot) {
			i++
			c.swap(numbers, i, j)
		}
	}
	c.swap(numbers, i, left)

	quickSort(numbers, left, i-1, c)
	quickSort(numbers, i+1, right, c)
}

func benchmark(n int) (*Comparer, *Comparer, time.Duration, time.Duration) {
	var start time.Time
	s := getRandomSlice(n)

	qComparer := &Comparer{}
	quickSlice := make([]int, len(s))
	copy(quickSlice, s)

	start = time.Now()
	quickSort(quickSlice, 0, len(quickSlice)-1, qComparer)
	quickTime := time.Since(start)

	hComparer := &Comparer{}
	heapSlice := make([]int, len(s))
	copy(heapSlice, s)

	start = time.Now()
	heapSort(heapSlice, hComparer)
	heapTime := time.Since(start)

	return qComparer, hComparer, quickTime, heapTime
}

func printLine(title string, list interface{}) {
	v := reflect.ValueOf(list)

	fmt.Printf("%v\t", title)
	for i := 0; i < v.Len()-1; i++ {
		fmt.Printf("%v\t", v.Index(i))
	}
	fmt.Printf("%v\n", v.Index(v.Len()-1))
}

func main() {
	test := []int{1000, 10000, 100000, 1000000}

	quickSwapCount := make([]int, len(test))
	quickCompareCount := make([]int, len(test))
	quickTime := make([]int64, len(test))

	heapSwapCount := make([]int, len(test))
	heapCompareCount := make([]int, len(test))
	heapTime := make([]int64, len(test))

	for j, t := range test {
		qs, qc, hs, hc := 0, 0, 0, 0
		var qt, ht time.Duration

		for i := 0; i < 10; i++ {
			q, h, qTime, hTime := benchmark(t)

			qs += q.swapCount
			qc += q.compareCount
			qt += qTime

			hs += h.swapCount
			hc += h.compareCount
			ht += hTime
		}
		quickSwapCount[j] = qs / 10
		quickCompareCount[j] = qc / 10
		quickTime[j] = qt.Microseconds() / 10

		heapSwapCount[j] = hs / 10
		heapCompareCount[j] = hc / 10
		heapTime[j] = ht.Microseconds() / 10
	}

	fmt.Println("Swap")
	printLine("#", test)
	printLine("Quick", quickSwapCount)
	printLine("Heap", heapSwapCount)
	fmt.Println()

	fmt.Println("Comparison")
	printLine("#", test)
	printLine("Quick", quickCompareCount)
	printLine("Heap", heapCompareCount)
	fmt.Println()

	fmt.Println("Running time")
	printLine("#", test)
	printLine("Quick", quickTime)
	printLine("Heap", heapTime)
}